Context Information
Table of contents
The Low-energy Chemical Space
For works based on computational chemistry one of the core challenges is the sampling of chemical space, i.e., the identification of structures that best describe the investigated system under given conditions. While there is no clear-cut, generalized definition of chemical space, in context theoretical chemistry it is sensible to relate the concept of chemical space to the potential energy surface (PES) of a molecule. The chemically intuitive understanding provided by this is that the molecular chemical space consists out of all relevant low-energy structures (minima on the PES) with respect to a similar composition or topology of the molecule. From a simplified point of view, this topology refers to all PES minima associated with a single two-dimensional Lewis structure of a molecule. An appropriate labeling would hence be low-energy chemical space.
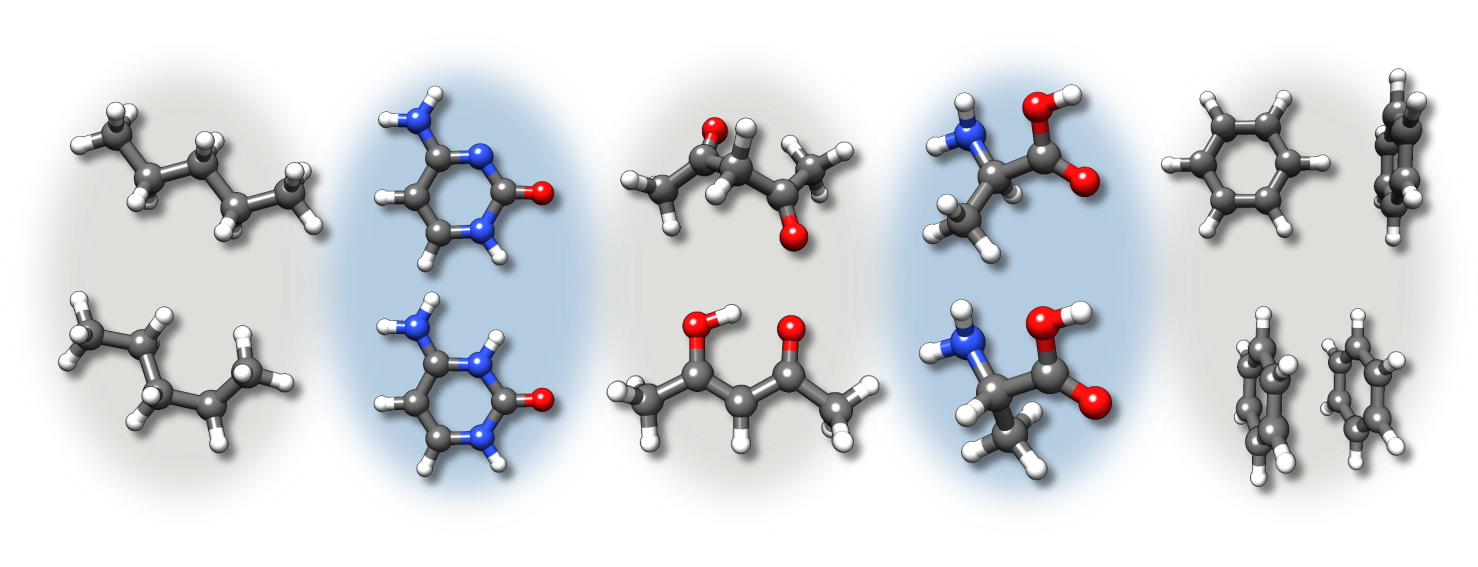
In a broader sense, the low-energy chemical space includes closely related isomers and chemical “derivatives” of a molecule. Most important isomers therein are conformers. Further contributing can be different protonation states, tautomers, or different non-covalent aggregation motives.
Conformers and Rotamers
Many physical observables are obtained as time average over the different low-energy structures of a molecule. The thermally accessible ensemble of minimum-energy structures generally consists of conformers as well as rotamers, i.e., spatial isomers of a molecule showing identical covalent connectivity and topology. Following the ergodic hypothesis, replacing the time average with an average over this so-called a conformer/rotamer ensemble (CRE) will in principle yield the same observables, while transforming the complicated time averaging into a managable sampling problem. Hence, in computational chemistry, it can be important to perform calculations on the favored conformation or an ensemble of conformations. Some examples for macroscopic observables that are depending on the molecular conformation, for example various spectroscopies (CD, NMR, IR), can be found in the Literature section.
By definition, conformers are the minima on a PES for a given molecular topology. Due to rotation around covalent chemical bonds (or other complicated inversion-type processes) that interchange nuclei belonging to the same group of nuclides the so-called rotamers arise. An example is the interchange of H nuclei at a methyl group due to its rotation. Rotamers have degenerate PES minima and thus are indistinguishable by any nuclear spin-independent quantum mechanical observable computed at the respective greometry. These definitions are depicted below.
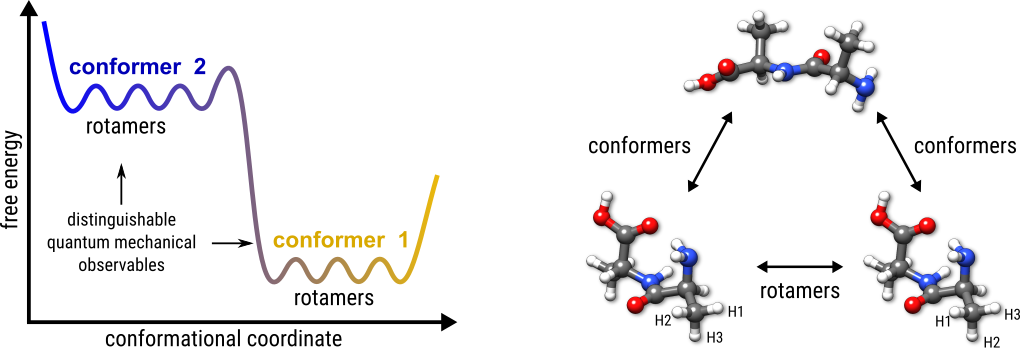
In practice we use three descriptors to distinguish between conformers and rotamers:
- The total energy
- The rotational constants of the molecule
- The Cartesian RMSD between two molecules
If two structures have completely different energies they are, by the above definition via the PES, different conformers. Otherwise, if they have the same energy within a chosen threshold, the structures could be either two different conformers with similar energies, two rotamers of the same molecule, or a duplicate of the same rotamer. In the first case (two conformers with similar energies) the RMSD will be high and the rotational constant will be different. For two rotamers the RMSD will be high, but the rotational constant is the same (within a chosen threshold). According to this criterium enantiomers (mirror image molecules) are a special case of rotamers. Only for duplicates of the same rotamer that have to be sorted out the energy and rotational constants will be identical while the RMSD is low.
The overall completeness of a CRE can be assessed by a maximized configurational or conformational entropy Sconf which, according to standard thermodynamical expressions, is proportional to the number of structures in the ensemble
\(S_\text{conf} \approx R \sum^\text{CRE}_{i} p_i \log p_i~.\)
In this equation R is the molar gas constant and the sum runs over all populations pi of all species with energy \(\Delta E_i\) at temperature T, given as
\(p_i = \frac{\exp(-\Delta E_i / RT)}{\sum^\text{CRE}_{j}\exp(-\Delta E_j /RT)}~.\)
The ensemble entropy Sconf is also linked to the ensemble free energy Gconf, which has to be minimized for a complete CRE.